Задача для поступления в 7 класс
Чтобы поступить в инженерный класс прославленной школы, нужно было решить одну из таких задач.
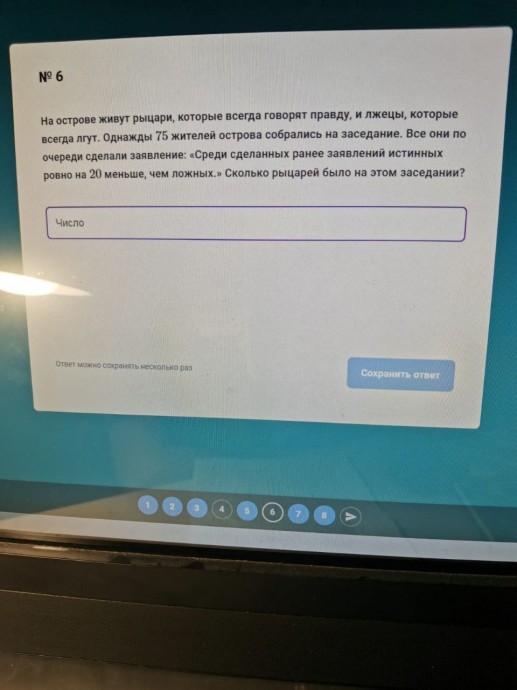
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Однажды 75 жителей острова собрались на заседание. Все они по очереди сделали заявление: «Среди сделанных ранее заявлений истинных ровно на 20 меньше, чем ложных.» Сколько рыцарей было на этом заседании?
П. С.: надоели ваши разборки.
И да, ответ я не знаю))
Все 75 лжецы. Рыцари вымерли, как динозавры, а врут абсолютно все, хоть и в малом))
А вдруг это какой-то остров, где ещё остались рыцари)) Типа Нарнии)
Рыцари вымерли когда закончились принцессы и драконы
Если рыцари всегда говорят правду, то первые 20 утверждений они не могут сделать, потому что ложных из них нет. Значит, осталось 75 − 20 = 55 человек. 55 рыцарей.
Я так вижу.))) Не знаю, правильно ли.
Сегодня показала эту задачу учителю математики. Тот сначала сказал, что надо решать через уравнение, но в итоге выяснилось, что 55 не делится на 2))) В общем понадобился листок, а его не было и учитель слился))
Сейчас посмотрим, может наши инженеры математики предложат ещё варианты
Я так и считал. 55 разделил на 2 и округлил в большую сторону, так как последний, 75-й говорит правду.
Задача будет решаться, если 21 будет первый рыцарь, не раньше не позже. Если 21 будет лгун, то он скажет правду. И дальше через одного будут они меняться, четные лгуны и нечетные рыцари. Потому можно считать от последнего 75 человека: x + x — 20 = 74, т.е. х = 47, количество лгунов. А рыцарей 28.
Внесу поправку, когда последний раз я закончил редактировать, сообщение Водяного уже было одну минуту, так что, он раньше написал правильный ответ)
а может там без если, это ведь 6 класс?))
х+(х-20)=75, а в конце правило округления.
75-48=27
Я исходил из того, что утверждение последнего рыцаря никто не оценивал)
такого вроде там не написано))
Ну там написано, что по очереди сделали заявление, т.е. скорее всего каждый делал по одному заявлению, а если рыцарь был последним, после него просто некому было это делать, если заявлений было всего по одному. Поэтому мне пришлось делать уравнение не по воображаемому 76 лгуну, а по настоящему рыцарю, ему как то больше доверия было)
Написано. 75 по разу высказались и всё.
21й точно первый рыцарь, без если, потому что он говорит правду.
Первые 20 ложные, 21 истинное, и дальше истинными будут каждое нечётное. Итого 28
Вашим детям очень повезло)
А тот ребёнок, что решал эти задачи не смог поступить в эту школу.
Тут надо учесть фразу: Среди сделанных РАНЕЕ заявлений (то есть на данный момент заявлений сделано уже на 1 больше)